Treatment Planning
Treatment Planning FAQ: Acuros XB Dose Reporting Mode
Which dose reporting method for AXB (and other MC-based algorithms) is best for clinical use: dose-to-water or dose-to-medium?
A resource for BED and EQD2: calculator, formalism, and pitfalls.
In a routine clinical environment, it can be difficult to determine the most effective fractionation for a patient undergoing treatment. Biological Effective Dose (BED) and Equivalent Dose in 2Gy Fractions (EQD2) are often used to quantify radiobiological concepts into concrete interpretable values. Here, we present a BED/EQD2 calculator and a brief background on the topic and its applications.
| Site | α/β Ratio |
|---|---|
| Kidney | 1.0 - 2.4 |
| Bladder | 3.1 - 7.0 |
| Lung | 3.9 - 8.2 |
| Brainstem | 2.0 - 2.1 |
| Prostate | 1.1 - 3.7 |
| Spinal Cord (Cervical) | 1.5 - 3.0 |
| Spinal Cord (Lumbar) | 2.3 - 4.9 |
| Bowel | 2.2 - 6.0 |
| Brachial Plexus | 2.1 - 4.1 |
| HN | 13.8 - 23 |
| Breast | 2.5 - 4.6 |
Hall, E. J. (2019). Radiobiology for the radiologist. In Radiobiology for the radiologist (p. 396). Philadelphia, PA: Wolters Kluwer. Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 1989 Aug;62(740):679-94. doi: 10.1259/0007-1285-62-740-679 . PMID: 2670032. van Leeuwen, C. M., Oei, A. L., Crezee, J., Bel, A., Franken, N., Stalpers, L., & Kok, H. P. (2018). The alfa and beta of tumours: a review of parameters of the linear-quadratic model, derived from clinical radiotherapy studies. Radiation oncology (London, England), 13(1), 96. doi: 10.1186/s13014-018-1040-z . PMID: 29769103. Kehwar TS. Analytical approach to estimate normal tissue complication probability using best fit of normal tissue tolerance doses into the NTCP equation of the linear quadratic model. J Cancer Res Ther. 2005 Jul-Sep;1(3):168-79. doi: 10.4103/0973-1482.19597 . PMID: 17998649.
Biologically Effective Dose—The Basics
Biologically effective dose (BED), as coined by the British Journal of Radiology some three decades ago, is an attempt to quantify the biological effect (log cell kill) of radiation dose delivery. The formula for BED was derived from the familiar linear-quadratic cell survival model:
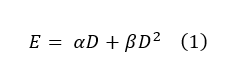
The equation determines the biological effect (E) as a function of dose (D), the linear dose damage response (α), and the quadratic dose response in tissue (β).
In general, cell injury can be classified into three categories.
- Lethal damage: unrepairable and will lead to cell death
- Sublethal damage: interactions that are not singularly lethal but can combine to result in cell death
- Potentially lethal damage: might be lethal at certain stages of the cell cycle and not fatal at others (e.g., unrepaired damage induced at the mitotic stage)
In the above equation, α represents irreparable lethal damage like double-stranded breaks, while β represents the damage done by two separate breaks or an accumulation of sublethal events. The variables can be manipulated in such a way to create a biologically equivalent dose, which can help compare clinical fractionation schemes by quantifying the biological effect of different schemes using a tissue-based variable (α/β ratio):
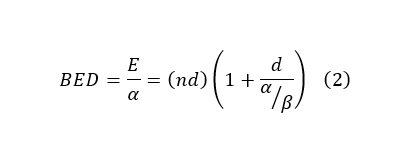
The α/β ratio represents the dose at which linear and quadratic components of cell killing are equal for a given tissue. A low α/β ratio (~3) indicates a late response, and a high ratio (~10) suggests an early response in tissue. In general, early responding tissue proliferates quickly while late responding tissues tend to be slower growing with a longer cell cycle. The fast proliferation in early responding tissue causes a majority of cells to spend time in the most radioresistant (S) phase. Increasing dose to overcome this can risk exceeding tissue tolerances, instead, treatments take advantage of a process called self-sensitizing. After irradiation, the surviving cells in highly proliferating tissues redistribute across other phases. By hyperfractionating, cells in radiosensitive phases are killed and then replaced by the surviving cells from more radioresistant phases. The second closely timed fraction, in turn, targets the newly redistributed cells. For late responding tissues (low α/β ratio), radioresistance arises from cells in early or resting radioresistant phases (G1, G0). Conventionally this is overcome using hypofractionated schemes might provide superior tumor control due to a more robust response in the linear portion.
Example
Suppose you want to compare hypofractionation vs. conventional fractionation and their respective effects on late (α/β = 3) and early (α/β = 10) responding tissues. The standard fractionation scheme is 180cGy x 44, and the hypofractionated is 250cGy x 28.
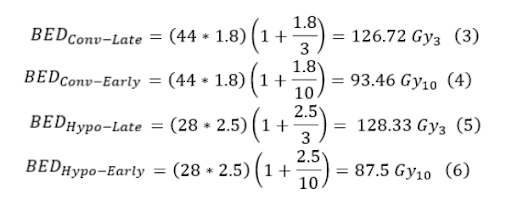
From equations three through six, it is seen that the conventional fractionation scheme is hotter for late responding tissue but colder for early responding tissue, so for early responding tissues, hypofractionation is superior. Now suppose we take a simplified HN case with an α/β = 10. Suppose you want to compare the conventional fractionation scheme of 200cGy x 30 with hyperfractionation of 110cGy x 70.
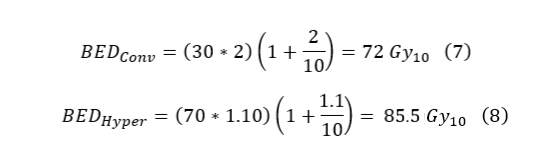
In this case, the hyperfractionated scheme delivers a more effective dose. In a more complicated prescription, a boost could be added to provide an additional dose. The total BED would just be the summation of each individual BED. It is important to note that if the boost were using brachytherapy instead of EBRT, the BEDs would still be summed; however, the brachytherapy BED requires a different formulation due to the significant damage repair during delivery.
Pitfalls
The basic BED formalism isn’t a perfect comparison of a fractionation scheme’s effectiveness. For example, the general expression assumes negligible incomplete cell repair between fractions and does not account for proliferation during treatment. This means significant breaks in treatment or accelerated cancerous cell proliferation could reduce the accuracy by as much as 1 Gy/day. Furthermore, BED relies on accurate α/β values. Published literature shows a high level of variance, even on the same site, due to clinical differences in treatment, differing tumor histology, and the subjective nature of specific endpoints and stages.
EQD2 Basics
With these limitations in mind, it is still a valuable tool in gauging a treatment’s effective dose delivered. In some cases, a BED might be desired, but in other cases, an alternative fractionation schedule is preferred. To aid in this, a similar formula called the Equivalent Dose in 2 Gy Fractions (EQD2) was developed to help convert the desired BED into a 2 Gy/fx scheme. This formulation provides a more practical way to view the effects of fractionation for most clinicians. The important difference between BED and EQD2 is that BED reports an effective dose, while EQD2 gives the equivalent dose needed in 2 Gy/fx to achieve that effective dose.
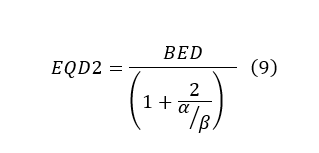
Using the previous example, suppose you want to figure out what 2 Gy fractionation scheme would give the same BED as the original prescription. If the BED = 96 Gy and the α/β = 10, then to achieve the same BED, a prescription of 200cGy x 80 would be needed. Since the EQD2 is just a derivation from BED and the LQ model, the pitfalls for both are still applicable. However, it does offer a powerful tool for clinicians to relate their empirical experience with a quantitative value.
Leave a comment